海盗分金问题、羊与车问题、一块钱哪儿去了⋯⋯或许大家都能背出这些经典问题的答案了,但国内论坛社区里仍然不停地转载这些谜题,标题越来越耸动,参与讨论的人也从未减少。那么,这些问题究竟是从哪里来的呢?
哪国人养鱼(Zebra Puzzle)
1. 一条街上有五座不同颜色的房子,每座房子住着不同国籍的人,每个人抽不同的烟,喝不同的饮料,养不同的宠物。
2. 英国人住在红房子里。
3. 西班牙人养狗。
4. 住在绿房子里的人喝咖啡。
5. 乌克兰人喝茶。
6. 绿房子就在乳白色房子的右边。
7. 抽流金岁月(烟名)的人养蜗牛。
8. 抽薄荷烟的住在黄房子里。
9. 住在中间的房子里的人喝牛奶。
10. 挪威人住在第一座房子里。
11. 抽契斯特菲尔德(烟名)的人住在养狐狸的人旁边。
12. 抽薄荷烟的人住在养马的人旁边。
13. 抽好彩(烟名)的人喝橙汁。
14. 日本人抽百乐门(烟名)。
15. 挪威人住在蓝房子隔壁。
那么,谁喝水?谁养斑马?
这个谜题已知的最早出处是 1962 年 12 月 17 日的《生活》(Life)杂志国际版上。1963 年 3 月 25 日,杂志公布了答案和世界各地数百个解决者的名单。这个谜题有无数的变种,其中一个就是网络上流传更广的“哪国人养鱼”。人怕出名猪怕壮,这个叙述繁琐的谜题竟莫名其妙地归功于了 20 世纪最聪明的大脑——爱因斯坦。此题乃“爱因斯坦年幼时所编”的说法广为流传,于是这个谜题也经常被叫做“爱因斯坦谜题”(Einstein‘s Puzzle)。但也有人说,作者其实是路易斯·卡罗尔(Lewis Carroll)。好吧,我们不要管这些追星族了,因为现在没有任何证据证明作者是他们中的任何一个。况且,谜题里的香烟品牌在爱因斯坦小时候还没有出现呢。
海盗分金谜题(Pirate Puzzle)
这是个流传很广的谜题,包含了诸如海盗、金钱、民主之类的流行元素。故事是这样的:有五个理性的海盗 A、B、C、D、E,他们得到了 100 个金币,要进行分赃。海盗世界等级分明,这五个海盗的排名如下:A > B > C > D > E。分赃制度也很民主:首先由等级最高的海盗提出一个分配方案,然后所有海盗(包括提议人)投票表决是否接受。若有半数或半数以上的人同意,则通过提议,否则把提议人扔下船去,由等级第二高的海盗接着提议,以此类推。海盗们考虑的因素如下:首先自己要活下去,然后要得到最多的钱;如果得到的钱反正都一样,他们更乐意把别人害死。
对于 A 来说,最佳方案是这样的:A 自己得 98,B 分得 0,C 分得 1,D 分得 0,E 分得 1。解答几乎出乎所有人的意料。一般我们都会把金币分给其他四个海盗以求他们通过提议而保住性命,而解答却告诉我们贪心更好。海盗谜题第一次出现在 1999 年 5 月的《科学美国人》上,文章标题为《海盗谜题》(A Puzzle for Pirate),作者是英国数学家伊恩·斯图尔特(Ian Stewart)。他详细地分析了这个问题,并把海盗的人数推广到 n 个,得到了十分有趣的结论。这个谜题是他从斯蒂芬·奥莫德罗(Stephen M. Omohundro)那儿听说的,据猜测,这个谜题已经流传了至少 10 年。
无论从哪个方面来看,这都是一道经典的谜题。在任何博弈论的课程中,都会讲到这个有趣的问题。
一块钱哪儿去了?
三个旅客住进一家旅馆,老板收了他们 30 元,每人 10 元。后来老板决定给他们一些优惠,给服务员 5 元让他退给旅客。很明显老板不会数学,给了个不能被 3 整除的数。聪明的服务员自己偷偷地藏下了 2 元,然后退给每个旅客 1 元。现在每个顾客优惠了 1 元,那么每人交了 9 元,一共交了 27 元,加上服务员的 2 元就是 29 元。可是一开始他们给了老板 30 元,那另外的一元到哪里去了呢?
几乎每个人看了之后都会上当,再看一遍之后还是觉得无比正确,再看一遍⋯⋯不少马大虎直到看了答案才明白过来,没想到这么简单啊。上网一搜,标题都是“一年级趣味数学”,自尊心大受打击。
这个谜题最早是从哪儿来的呢?在中文网络中最流行的说法是,这个谜题来自一道“新西兰面试题”,真实性等待谣言粉碎机鉴定。事实上,这个问题的历史可能比大家想象的要长得多,它至少可以追溯到加利福尼亚大学 1949 年出版的数学课本中,而最早的出处恐怕已经不得而知了。
这个“悖论”的成功得益于 27 + 2 = 29 跟 30 相差无几(若是相差太大必然会引起怀疑),想象力丰富的听众还没弄明白是两个什么东西加了起来,就开始浮想联翩了。谁知道这个算式本身就是错的,2 元已经包括在 27 元里面了,27 - 2 = 25 就是老板手里的钱,并没有少。
后来人们给出了一个专属于这个谜题的解答,自嘲当初的失误:“几个月后,其中的两个旅客又住进了这家旅馆,老板收了每人 10 元,一共 20 元。后来他又想给旅客优惠,又是 5 元;然后又是那个服务员,不过这次他扣下了 3 元,还给旅客每人 1 元。现在每个旅客交了 9 元,合起来是 18 元,加上服务员的 3 元,一共 21 元。看,少了的那 1 元在这里”。
不可能完成的谜题(Impossible Puzzle)
有两个不相等的整数 x,y ,它们都大于 1 且和小于 100 ,数学家“和先生”知道这两个数的和,数学家“积先生”知道这两个数的积,他们进行了如下对话:
积先生:我不知道 x 和 y 分别是啥。
和先生:我知道你不知道。
积先生:我现在知道了。
和先生:如果你知道了,那我也知道了。
那么,x 和 y 各是多少?
现在知道为什么这叫做不可能完成的谜题了吧,因为光看这几句“废话”我们似乎根本不可能算出 x 和 y 来。1969 年,荷兰数学家汉斯·弗莱登塔尔(Hans Freudenthal)发表了这个谜题,当时被称为“弗莱登塔尔问题”(Freudenthal Problem)。直到 1976 年大卫·斯布罗斯(David Sprows)在《数学杂志》(Mathematics Magazine)上才给出了这个问题的英文版本。1979 年,马丁·加德纳(Martin Gardner)在他的专栏上又一次提到了这个谜题,并称它为“不可能完成的谜题”,之后这个问题就开始大红大紫了。它有无数个变种,并广泛流传。题目描述看似简单,解答却并不简单。图灵奖获得者艾兹赫尔·迪杰斯特拉(Edsger W. Dijkstra)说他在 1978 年曾经解决了这个问题的另一个版本。之前他无数次尝试心算解决它却屡屡入睡,终于在一个无眠的夜晚,花了六个小时,硬是没有用纸和笔,在脑子里解决了那个问题。在证明过程中,他还小小地用了一下哥德巴赫猜想。
失踪的正方形(Missing Square Puzzle)
这个谜题不需要介绍,图已经说明了一切。上面的三角形中少了一个小格,它去了哪里?
马丁·加德纳说这是由纽约业余魔术师保罗·嘉理(Paul Curry)在 1953 年发明的,所以也称为“嘉理悖论”(Curry’s Paradox)。所有像嘉理悖论这样的谜题都被叫做“裁剪悖论”(Dissection Paradox)。马丁·加德纳在他的《数学,魔术和秘密》(Mathematics Magic and Mystery)中介绍了另一个类似的悖论,叫做虎珀悖论(Hooper’s Paradox),由数学家威廉·虎珀(William Hooper)在他 1774 年出版的《理性的娱乐》(Rational Recreations)中提出。后来经道格拉斯·罗杰斯(Douglas Rogers)教授调查,虎珀悖论其实最早出自 1769 至 1770 年间法国作者吉尔斯·盖特(Edmé Gilles Guyot)出版的论文集《新奇的物理和数学娱乐》(Nouvelles récréations physiques et mathématiques)里。
史上最难的逻辑谜题(The Hardest Logic Puzzle Ever)
有三个精灵,一个只说真话,一个只说假话,另一个随机说真话或者假话。你可以向这三个精灵问三个是非题,每次问谁都可以,下一个问题可以根据上一个问题的答案来问。你的任务就是判断他们的身份。不幸的是,他们可以听懂你的话,却用他们的方言—— Da 和 Ja ——来回答。你不知道那个表示对,哪个表示错。那么,你应该问哪三个问题呢?
这个标题党要归功于麻省理工学院的逻辑学家乔治·史蒂芬·布罗斯(George Stephen Boolos)。1996 年,他在《哈佛哲学评论》(The Harvard Review of Philosophy)发表了同名文章,文章中说这个谜题是由美国数学家雷蒙德·斯穆里安(Raymond Smullyan)发明的。谜题看上去有点绕,其实事情原本没有这么复杂。斯穆里安曾经提出过这个问题的简化版本“骑士与流氓”(Knights and Knaves),里面没有情绪不稳定的第三者,而且他们说的话你也听得懂。后来有人嫌这个不够难,就加了“你听不懂他们的话”这个条件。这个人就是图灵奖获得者约翰·麦卡锡(John McCarthy)。再后来,题目又多出了一个第三者,这样便算得上是“史上最难的逻辑谜题”了。这些相关的谜题都可以在斯穆里安的《这本书叫什么名字》(What is the name of this book)和《舍赫拉查德的谜题》(The Riddle of Scheherazade)中看到。
蒙提霍尔问题(Monty Hall Problem)
假设你参加一个电视游戏节目,节目现场有三扇门,其中一扇门后面是一辆车,另外两扇门后面则是山羊。主持人让你选择其中的一扇门。不妨假设你选择了一号门吧。主持人故意打开了另外一扇门,比如说三号门,让你看见三号门的后面是山羊。然后主持人问你,“你想改变你的选择,换成二号门吗?”这时候,你会怎么做?
这个游戏最早出现在美国的电视游戏节目《Let’s make a deal》中。1975 年,史蒂夫·塞尔文(Steve Selvin)教授在《美国统计学家》(American Statistician)上发表文章,把这个问题称为“蒙提霍尔问题”(Monty Hall Problem),因为那个节目主持人就叫蒙提霍尔(Monty Hall)。玛丽莲·沃斯·莎凡特 (Marilyn vos Savant),吉尼斯世界记录认定的最高 IQ 人类,在《Parade》杂志上开了一个名叫“问问玛丽莲”(Ask Marilyn)的专栏,专门回答读者各式各样的问题。1990 年,一个叫 Craig F. Whitaker 的读者给这个专栏寄去这个问题,玛丽莲是这样解答的:“坚持选一号门赢的概率是 1/3,但换成二号门赢的概率是 2/3,因此你应该换一扇门。设想下面的情况,有 100 万扇门,你选了一号门之后,知道内幕的主持人打开了除了二号门之外所有其它的门,你必然会果断地改变选择,是不是?”这个解答发布后,引起了巨大的争议,因为这大大违反了人们的直觉。甚至有不少大学博士去信“纠正”她的错误,理由是:主持人开了一扇门之后,剩下一辆车和一只羊,概率显然变成了 1/2 。他们督促玛丽莲“承认错误”,有人甚至表明自己“为美国的未来担忧”,这些记录至今还留在 玛丽莲的网站 上。大家不妨去参观一下,看看有多少 PhD 栽了跟头。
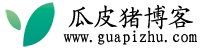


2011年05月8日 2:47 下午 沙发
这个是我从网上看到的,觉得很有意思,就发过来了。也可以活跃下自己的大脑。